Expectations, Probability and Uncertainty

As actuaries, we are constantly dealing with expectations. Our expectations of future uncertain outcomes dictate how behavior and decision-making determine the economy’s operations.

It may appear that I am preaching to the choir. Still, this article contrasts expectation theory (learned from mathematics, mainstream and behavioral economics) with neuroscience’s depiction of how people make decisions—which can lead to new mathematical techniques and a more realistic way of understanding expectations.

Why Is This Essential to Actuaries?

As Austrian-British economist and philosopher Friedrich Hayek stated in his “The Use of Knowledge in Society” writing in 1945: “Any approach, such as that of much of mathematical economics with its simultaneous equations, which in effect starts from the assumption that people’s knowledge corresponds with the objective facts of the situation, systematically leaves out what is our main task to explain. I am far from denying that in our system equilibrium analysis has a useful function to perform. But when it comes to the point where it misleads some of our leading thinkers into believing that the situation [that] it describes has direct relevance to the solution of practical problems, it is high time that we remember that it does not deal with the social process at all and that it is no more than a useful preliminary to the study of the main problem.”¹

Hayek lays out (brilliantly, in my opinion) that understanding economics and market uncertainties means recognizing how society and people acquire knowledge and make decisions—important, in my opinion, for actuaries. The equilibrium analysis embedded in risk metrics has little direct relevance to the practical problem of dealing with future uncertain outcomes, which should be our primary goal, I assert as an actuary.

Expectations: A Review

As I’ve learned, expectations come from probability theory. The key to probability is understanding that it comes with an event space containing all the possible outcomes for an event. For example, pretend we are calculating the probability of rolling a five on a six-sided die. The event space is the numbers one through six. The event is five for a probability of 1/6. The expectation is just weighting each event by its respective probability, such as  , where p is the probability of each side and x is the number on each side. The expectation of a six-sided die is: 1*1/6 + 2*1/6 +3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = 3.5.

As you can see from the example, a crucial property is required for expectation to work. You must know all the possible events and their corresponding probabilities in the event space with certainty. It is the fixed membership of the event space that translates into the requirement of knowing all future outcomes with certainty. All types of risk in general also have this shortcoming, meaning risk and expected value are directly related. This shortcoming is genuine regardless of whether you calculate expectations with objective or subjective probabilities.

• Objective probabilities are derived from the frequency of events, like in our example.²
• Subjective probabilities are probabilities derived from personal judgment or experience.³

There is a deep, long-standing, philosophical debate about which is better. I will save you the pain of understanding the arguments because neither one overcomes the requirement of knowing all possible future outcomes in the event space with certainty.⁴ It’s six of one and half a dozen of the other.⁵

Uncertainty and Probability Don’t Mix

As stated, risk calculation requires all possible future outcomes to be known and fixed, which does not allow for the novelty of new outcomes. For example, the probability of seeing an airplane fly overhead in 1850 is zero because airplanes didn’t exist. In 2024, it is far greater than zero. How can actuaries adjust their methods to account for the uncertainty and novelty of future events? Novelty would need the event space to be constantly adjusted, which means probability is a poor metric in an uncertain setting.⁶

I would like to summarize the forming of expectations in different settings:

• How might expectations be formed at a casino? The same as probability theory and risk theory in economics and finance—casinos define the rules and hold the event space constant.
• How might expectations be formed in the uncertain real world where insurance is sold? They can’t be, I assert, since we cannot know the underlying future event space with certainty.⁷ The event space continuously changes in an uncertain world due to universal innovation.⁸

The domain of novel, uncertain future events includes past known events, which implies they are much larger than past known outcomes alone.⁹ Therefore, I believe humans form suppositions—not expectations.

Supposition

A common definition of supposition is “an uncertain belief.” I will slightly massage this to “beliefs in future uncertain outcomes based upon current and past knowledge.” Now, supposition better aligns with what economics, finance and actuarial science are trying to accomplish.

In the expectation theory framework, prices are nothing more than the supposition of future availability, need and desire for a particular commodity or service. The supposition is a far more challenging problem, so mainstream economics avoids it.¹⁰ But, ironically, this avoidance to me invalidates mainstream theory and gets in the way of the ability to understand how the perceptions of future events unfold.¹¹

Reconciling Suppositions and Expectations

One might be considered dismissive of the “Suppositions and Expectations” discussion if their first inclination is to quote “All models are wrong, but some are useful,” from British statistician George E.P. Box’s 1976 paper “Science and Statistics.”¹² Furthermore, prospect theory explains how people make decisions involving risk. In simple terms, it suggests people don’t always act rationally when making choices. It is easy to show through prospect theory that decisions based on risk will be wrong when made in an uncertain setting,¹³ degrading the practicality of behavior finance and economics to outside disciplines trying to explain natural phenomena.

In the podcast People I (Mostly) Admire, episode 126, economist and co-author of “Freakonomics” Steve Levitt states: “And [behavioral economics is] really a one-way journey. What has happened is psychologists and economists have found things in psychology and imported them into economics. The opposite just hasn’t happened. There hasn’t been this reverse transference. Honestly, thinking about it now, I’m not exactly sure why that is the case.”

Behavioral economics and finance try to bring psychology into economics. Then they question why they do not align, but mainstream economics forced them to do this to get buy-in.¹⁴ People evolved to deal with uncertainty and not risk. Cognitive disciplines agree with Hayek that no one should assume anyone has any particular knowledge about a situation. Therefore, they have little use in the results, which I believe is the source of Levitt’s bewilderment. I can see no reason that economics should not reconcile its models with other social and cognitive disciplines.

I believe there are two significant pieces to understanding supposition:

1. How does the brain learn and acquire knowledge to form suppositions?
2. How does the brain use this knowledge to plan for novel future environments?

Acquiring Knowledge Through Brain Maps

Brazilian neuroscientist Suzana Herculano-Houzel explains that we are the only animals that cook our food, which allows us to extract far more calories from the food to feed our brains. The 86 billion neurons in our brains require 512 kCal/day, which is 2% of our body mass but 25% of our body’s energy consumption. We are the most intelligent animals on Earth because we have the most neurons, but it comes at an energy premium.¹⁵

Brain Maps

Not only is energy at a premium but so is space. Neurons must communicate with each other, which they do through dendrites and axons. If all the neurons were connected, your brain would be 12.5 miles wide to house the thinner-than-hair connections!¹⁶ The brain deals with all these limitations by building maps to model the world and keep track of your place within it. The models are not exact snapshots but abstractions, allowing information compression to what is necessary. These abstractions increase the speed and clarity of our senses, detecting and correcting inevitable errors and omissions in information received from them. Optical illusions occur due to this error-correcting process.¹⁷

This sensory information abstraction is excellent for dealing with the physical world. But how does the brain handle abstract concepts like uncertainty, conflicts, time and, most importantly, actuarial science? The brain combines the maps our senses use in new and novel ways. For example, cultures that read from left to right will have the concept of lesser on the left and more on the right, and vice versa for cultures that read from right to left. Hence, your spatial and visual maps help define magnitude.¹⁸

Abstractions

In her book, The Joy of Abstractions: An Exploration of Math, Category Theory, and Life, Eugenia Cheng explains that: “Abstraction is the process of deciding on some details to ignore to ensure that our logic works perfectly. Mathematics relies heavily on abstraction to get it going. Its arguments are all based on rigorous logic, and rigorous logic works in abstract settings. In normal life situations, there is always the possibility that something will get in the way of logic working perfectly. The idea is that abstraction itself has the potential to be ambiguous, and category theory provides a sector framework for performing abstractions.”¹⁹

Furthermore, Cheng states: “There is a competition between set theory and category theory as the foundation of all mathematics. Set theory starts with membership as a basic concept and builds up from the idea of elements being members of sets. By contrast, category theory builds up from the notion of relationships, which is why the basic concepts in category theory are elements (objects) and relationships between them rather than membership. It is the difference between looking at intrinsic characteristics versus behavior in different contexts. However, a more mathematical ideology is that category theory takes sets and functions as the primary starting point rather than sets and membership.”²⁰

From the merging of brain maps and category theory, I will extrapolate that nature decided that category theory won the debate on the foundation of mathematics. The beauty of using abstractions is that they can easily be recombined in novel ways to create new abstractions and relationships to adapt to the world’s uncertainty. Using abstractions minimizes energy and space because abstractions can better adapt to new and changing environments as needed and compress knowledge and energy requirements for storage. Furthermore, this eliminates the requirement of knowing all future outcomes, which is not physically possible.

Using Knowledge in Novel Environments

A group of closely proximate neurons creates a brain map, an abstract representation of your environment. Neurons have 1,000 to tens of thousands of synapses spaced along the branches of the dendrites. The dendrites receive signals from other cells and are the hub of connectivity for each cell. The synapses are the connections to other neurons.²¹ As we learn, the synapses strengthen connections between neurons and brain maps. When a synapse is thicker, this makes the electrical current between two neurons flow more easily.²² This thickness of a synapse encodes the possibility that the connected neurons are related because the relationships are likely vague and not absolute. The easier the flow of electricity, the greater the possibility.

Probability Versus Possibility

Possibilities and probabilities are different but complementary concepts, so they are not synonymous.²³ Possibility theory derives from fuzzy mathematics. As Apostolos Syropoulos and Theophanes Grammenos cover in their book, A Modern Introduction to Fuzzy Mathematics:

• Probability theory is a natural tool for formalizing [risk] when class frequencies are known.
• Possibility theory is a natural tool for formalizing uncertainty resulting from imprecise and fuzzy information.

Fuzziness is the ability to have uncertainty in belonging to a mathematical structure, defined as vagueness. It defines crispness as entirely belonging to a set,²⁴ abstraction, relationship or other mathematical structure. Fuzziness provides weights from [0,1], specifying the vagueness degree. Probability and possibility have weights from [0,1], so they are commonly confused with each other.²⁵

The brain does not directly deal with probabilities—but possibilities—because, to me, it does not care about the likelihood of an event occurring. Your brain—and you, if you ponder for a second—care about identifying the possible relationships and abstractions to which the incoming information belongs. If you’ve dealt with the situation before, then you know the correct behavior.

For example, if you understand the event, you can determine how to handle the situation or slightly adapt brain maps to accommodate its novel pieces. Maybe probability then comes into play as an available abstraction of the problem. If you do not understand the event, it is possible to flee it. Therefore, I believe the brain is not a prediction engine but a relational engine. It does not need to figure out what will happen to take action—the brain needs to relate new information to existing experiences to determine proper behavior.

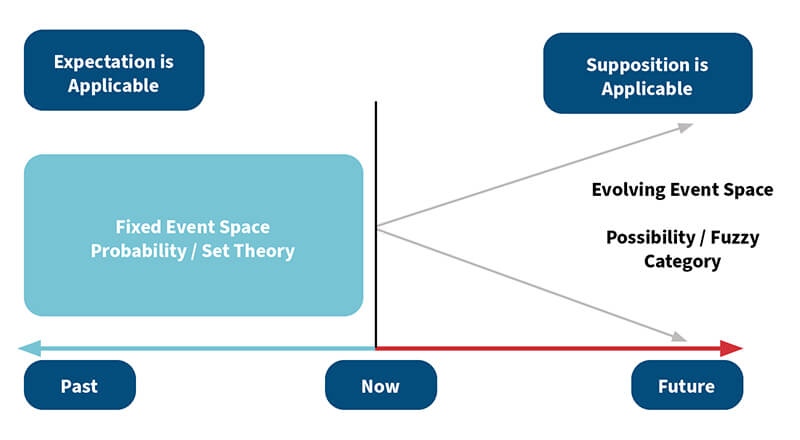
The Bottom Line

In economics and finance, how people perceive the future can dictate how markets behave, which is the basis of the expectation of current financial values. This article has attempted to show the disconnect between the theory of how we model expectations and the reality of their formations as suppositions, which are beliefs in future uncertain outcomes based on current and past knowledge.

For mathematics to viably handle uncertainty, it cannot assume that the event space is fixed in the future. It must handle the fact that living systems innovate, adapt and evolve, which means the event space is bound to change.

I believe it is important to reach an understanding of how the brain copes with uncertainty. The brain uses maps, which are abstractions of the world. The study of abstractions and their relationships is the subject of category theory, which could replace set theory to migrate from calculating expectations to suppositions. Furthermore, I assert that possibility weights are better than probabilities for weighting the relationships between applicable abstractions. Introducing these newer mathematical ideas into risk metrics could better explain how people determine suppositions and future economic outcomes.

Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries or the respective authors’ employers.

Copyright © 2024 by the Society of Actuaries, Chicago, Illinois.