Money, Value and GameStop

Quantum economics is applicable to actuaries. Insurance organizations collect premiums from policyholders and likely invest a portion in illiquid, long-dated assets, which have no active market to determine their current price. The liabilities that insurance companies sell are illiquid and will never be for sale on a market exchange. Yet, all the latest accounting regimes are moving toward a market-consistent valuation of insurance assets and liabilities.

In neoclassical economics, price and value are assumed to be equivalent, which makes modeling and determining the price for these assets and liabilities difficult. (There are methods to find equivalent liquid securities to replicate and price the illiquid securities, but they are based on optimistic assumptions.) Quantum economics is designed to better deal with illiquid assets by realizing that price and value are two concepts based on quantum mechanical models, which are mathematical models that describe physics regarding information, measurement and uncertainty at the tiniest levels .

This article is my attempt to apply the concepts of quantum economics to a recent phenomenon as a way to encourage actuaries to become energized about the topic. Quantum economics is a deep subject rich with new ways of studying option theory and policyholder behavior through quantum cognition—and this article will only scratch the surface. With little to no mathematics, this article will first describe quantum and classical mechanics basics. Then it will demonstrate similarities between quantum mechanics and economics through a memorable example: the January 2021 GameStop short squeeze event.

Classical and Quantum Measurement, Information and Uncertainty

Whether the subject is classical or quantum mechanics, information, measurement and uncertainty are intimately related. It is worth taking the time to understand the concepts relative to physics because it will make the ideas in economics easier to understand.

Information

In classical physics, information comes in bits—either off or on, happened or didn’t happen, or 1 or 0. It is all or nothing. In quantum mechanics, a quantum bit (qubit) captures the quantum information, which can be in a superposition of 0 and 1. The qubit encodes the data you observe, such as spin, position or momentum. When an observable is in superposition, it is in two states simultaneously (i.e., duality).

A qubit is not a thing: It is a mathematical concept. It is a coordinate system, just like in introductory algebra. Even though we are talking about natural objects like electrons and photons, the remarkable aspect of the coordinate system is that it is in the imaginary plane.¹ In other words, your x-axis is a real number and your y-axis is an imaginary number.

Measurement

Before measurement in quantum mechanics, the observable is in a superposition, which means it is somewhere within its imaginary coordinate system. When you hear that the measurement collapses the waveform, it sounds odd and mysterious. The collapse means that measurement caused the observable to move from the two-dimensional, imaginary plane to a one-dimensional, real number.² This collapse causes something further and more foundational: It causes quantum information (qubit) to become classical information (bit), connecting quantum and classical information.³

Uncertainty

Classical physics and quantum mechanics intimately tie information and uncertainty together differently. Classical physics has a positive amount of uncertainty relative to how the experiment will turn out before the investigation runs. After the experiment, measurement causes the amount of uncertainty drained to equal the information gained.⁴ In classical physics, information and uncertainty are two sides of the same coin.

Heisenberg Uncertainty Principle

Quantum mechanics intimately relates quantum information to the Heisenberg Uncertainty Principle. The Heisenberg Uncertainty Principle implies that gathering information about two complementary variables or observables, such as position and momentum, will cause a loss of information about the other.⁵ As we will see later, this is also true for a stock’s position and momentum—that is, stock price and change in stock price, respectively.⁶

For example, imagine an electron: It can spin up and down or left and right. The up-and-down spin complements the left-and-right spin, so the spins have individual coordinate systems. Suppose I set the electron into motion with an upward spin when I experiment. Now, if I measure for the upward spin, then with certainty, the measurement will indicate that I did this. But what happens if I measure the complementary left-and-right spin? The results will be uncertain because the measurement perturbed the system. Sometimes, the spin will be left and occasionally right, which has an associated probability distribution with this outcome.

Quick Mental Note

To summarize the critical points, if the experiment is performed and measured—but it does not affect the results and the measurement order is immaterial—then it is classical physics. On the other hand, it is quantum mechanics if, before experimenting, the observable is in a superposition, the measurement affects the results and the order matters. What does this have to do with economics?

Quantum Economics and Money

Neoclassical economics has a misunderstanding in that it leaves money out of financial transaction modeling. It downplays the importance of money by treating it as a substitute for barter. The perspective that money is a passive medium of trade dictates that price is always equal to value.

Quantum economics is the new science of money. Contrary to neoclassical economics, quantum economics places money at the heart of the economy with a first-class status. Quantum economics recognizes that there is a distinction between price and value. Before a transaction, value is a fuzzy, indeterminate quantity,⁷ which, for simplicity, is in a superposition of execute or not execute. It is not until a transaction is made (same as a measurement) that the waveform collapses and the price is determined.⁸ Money is a physical representation of this duality that can be an abstract number like a credit amount or a physical manifestation like a coin.⁹

Let us go back to my earlier comment about a stock having two complementary values: stock price and change in stock price (stock price velocity). Explaining this concept is best done through the age-old battle between fundamentalist and technical analysis when finding the value of a company and its stock.

Fundamentalist and Technical Analysis

The fundamentalists believe that the analyst needs to look at financial health, economic indicators, industry trends, management teams and other qualitative and quantitative factors to find the value of a business. The idea behind fundamental analysis is that the intrinsic value of an asset can be estimated based on these factors. In other words, fundamentalists look at the current position of the company to derive its value.

On the other hand, technical analysts focus on studying historical price and volume data of financial instruments, such as stock charts, to identify patterns and trends. Technical analysts believe that market prices reflect all relevant information, including fundamental factors, and that historical price patterns can help predict future price movements. In other words, technical analysts look at the velocity or momentum of the stock to derive its value.

Heisenberg Uncertainty Principle Revisited

Here is the key to the puzzle: Quantum economics shows that fundamentalists and technical analysts are both right and wrong! Fundamentalists and technical analysts hold complementary values in which measurement affects the results. It would be best to look no further than the GameStop short squeeze example to see this in full, vivid display.

Figure 1 shows the five-year average of the stock price from finance.yahoo.com.

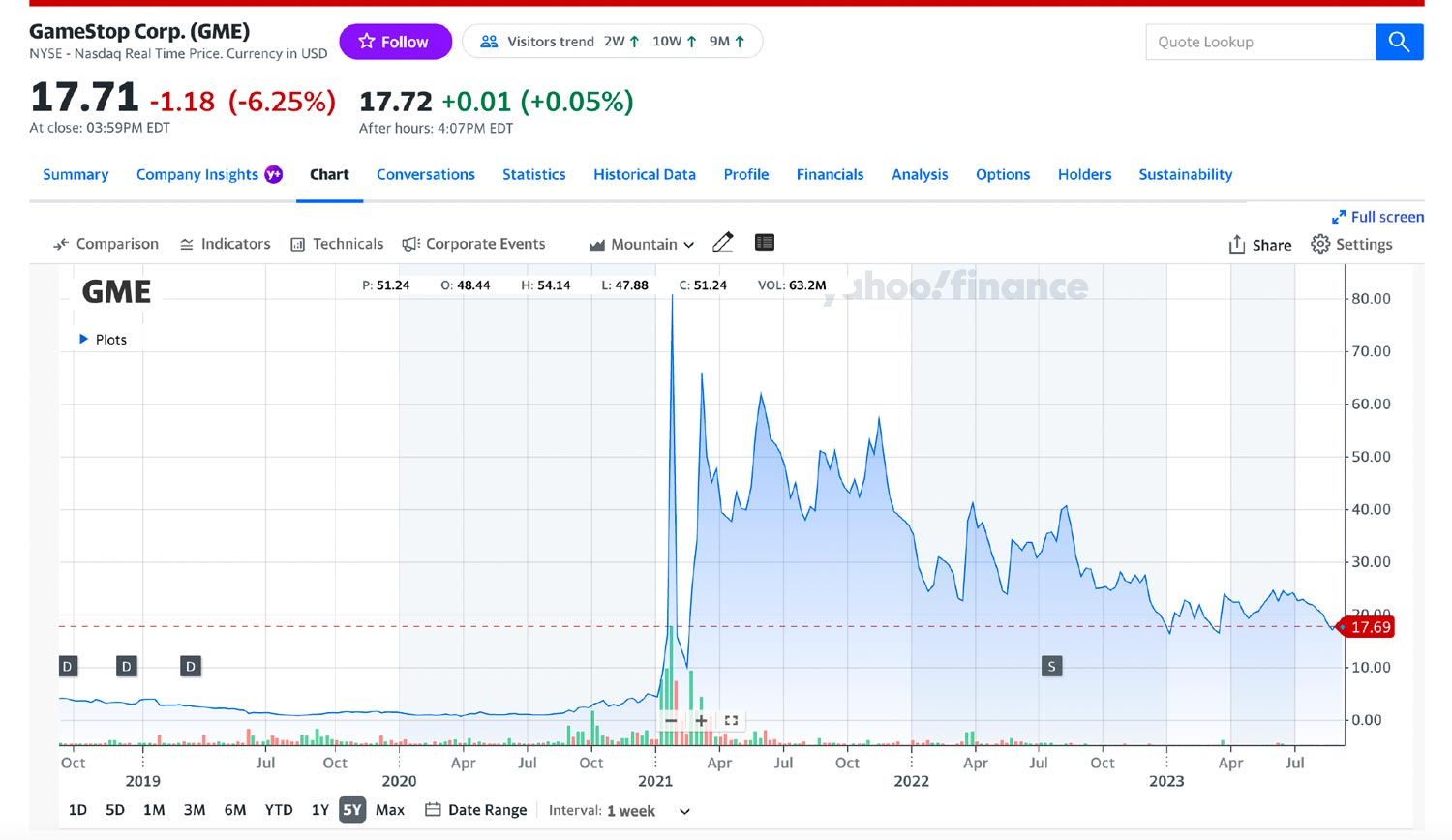
Before the COVID-19 pandemic, GameStop (GME) was a struggling company. Its fundamentals were weak, so hedge funds started shorting the stock based on poor position. At the same time, online traders—pseudo-technical analysts—began talking about the company and hyping it up, increasing the stock’s velocity and sending the stock’s value on a wild ride.

This scenario makes no sense in a neoclassical view of the economy because the price should reflect all previous information and future expectations. Furthermore, the returns are far from a Gaussian (normal) distribution. Figure 2 is a Q-Q plot of the GME returns. If the returns are Gaussian, all the points should be on the red trend line.

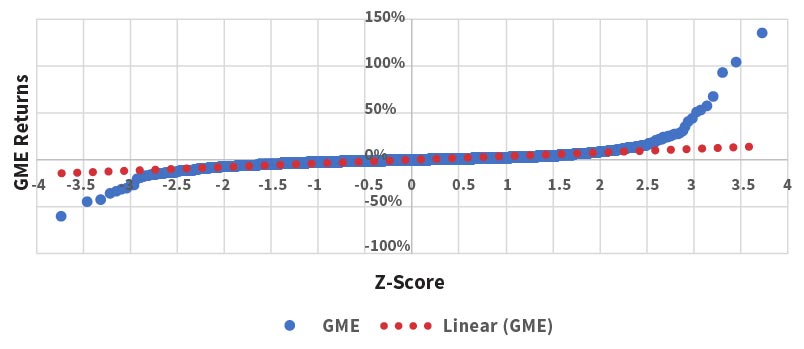
On the other hand, the GME short squeeze makes perfect sense in quantum economics and under the Heisenberg Uncertainty Principle. Embedded in the fundamentals are intangible assets, such as trademarks, franchises, goodwill and brand equity, which are fuzzy, indeterminate values based mainly on hype and brand recognition. The more the technical analysts gathered and shared information about the momentum of the GME stock, the less information hedge funds knew about the position of fundamentals due to the intangible assets. The measurement of one complementary value disturbs the other, which makes it impossible to have complete information about both simultaneously.

In neoclassical economics, there is no difference between price and value, so both parties thought they knew the value, not recognizing that each was holding the other’s compliment. Quantum economics recognizes how different quantities complement and affect one another, leading to uncertainty in GME value. The hedge funds did not account for this additional uncertainty, which destroyed their anticipated gains.

As the two groups measured the stock value, they forced the value’s waveform to collapse from the imaginary-number plane into the real-number stock price. When the actual stock price is determined, the information gained about the intangibles equals uncertainty drained.

The Bottom Line

Quantum economics gives us a new perspective on understanding economic phenomena, which neoclassical economics struggles to explain. Neoclassical economics treats money as if it is just a replacement for barter, but quantum economics puts money front and center. The significant difference is that quantum economics separates price from value.

Quantum economics derives its models from quantum and classical mechanics concerned with information, measurement and uncertainty. Value is modeled with quantum mechanical concepts while price is modeled with classical counterparts. Just as the qubit collapses into a classical bit upon measurement, the value of an item, such as stock, collapses to its price upon measurement. Furthermore, the measurement of complimentary values leads to Heisenberg Uncertainty.

Lastly, quantum economics provides a unique way to look at the GameStop short squeeze in 2021, which the Heisenberg Uncertainty Principle can explain. During the short squeeze, the hedge funds valued GME relative to the company’s financial position. The online traders priced GME by the stock’s momentum. When measuring these complementary values, the more information gained about one, the less is known about the other. The measurement process disturbs the complementary values, making it impossible to know them simultaneously. The hedge funds did not account for this additional uncertainty, which destroyed their anticipated gains.

Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries or the respective authors’ employers.

Copyright © 2023 by the Society of Actuaries, Chicago, Illinois.